Cryptography at Riptides

Modern infrastructure demands strong, scalable, and transparent identity, especially for non-human actors such as services, workloads, jobs, and agents. Riptides introduces a novel approach by anchoring non-human identity directly in the kernel, leveraging SPIFFE, kTLS, and in-kernel mTLS handshakes to deliver zero-intrusion security - combining identity and encrypted communication seamlessly for user-space applications.

To realize this approach, Riptides builds on proven cryptography, specifically TLS. At its core, TLS relies on keys, certificates, encryption, digital signatures, and key exchange. In this post, we’ll walk through the fundamentals of these building blocks: symmetric cryptography, asymmetric cryptography (RSA and Elliptic Curve Cryptography), digital signatures, and key exchange. We’ll also share rough comparisons from Riptides using different key types to highlight the trade-offs in practice.

What is Cryptography?

The word cryptography comes from the Ancient Greek kryptós, meaning “hidden” or “secret.” At its core, cryptography is the science of protecting information, allowing people (and machines) to communicate securely, even in the presence of adversaries. A simple analogy is a locked treasure chest: only someone with the correct key can open it.

Cryptography underpins almost everything in the digital world, from online banking to AI agents exchanging data across networks. This post isn’t meant to be an exhaustive guide, but rather a focused introduction to the essentials. One of the central challenges is ensuring that data can be transmitted so only the intended recipient can read it and no one else.

TLS Requirements

Transport Layer Security (TLS) is the backbone of secure communication on the internet. At a high level, TLS guarantees three critical properties:

• Confidentiality: Only authorized/intented recipients can read the data.
• Integrity: Any tampering with the data is detectable.
• Authentication: The parties involved can prove they are who they claim to be, and can verify each other’s identity.

To deliver on these guarantees, TLS combines several cryptographic building blocks:

• Encryption: Keeps the content of messages private (using both symmetric and asymmetric encryption).
• Digital Signatures: Ensure authenticity of messages and certificates.
• Key Exchange: Securely establishes/agrees a shared secret between parties.
• Certificates: Bind public keys to verified identities, enabling trust.

In the next sections, we’ll look at these components in more detail, starting with symmetric and asymmetric cryptography - the foundation of TLS.

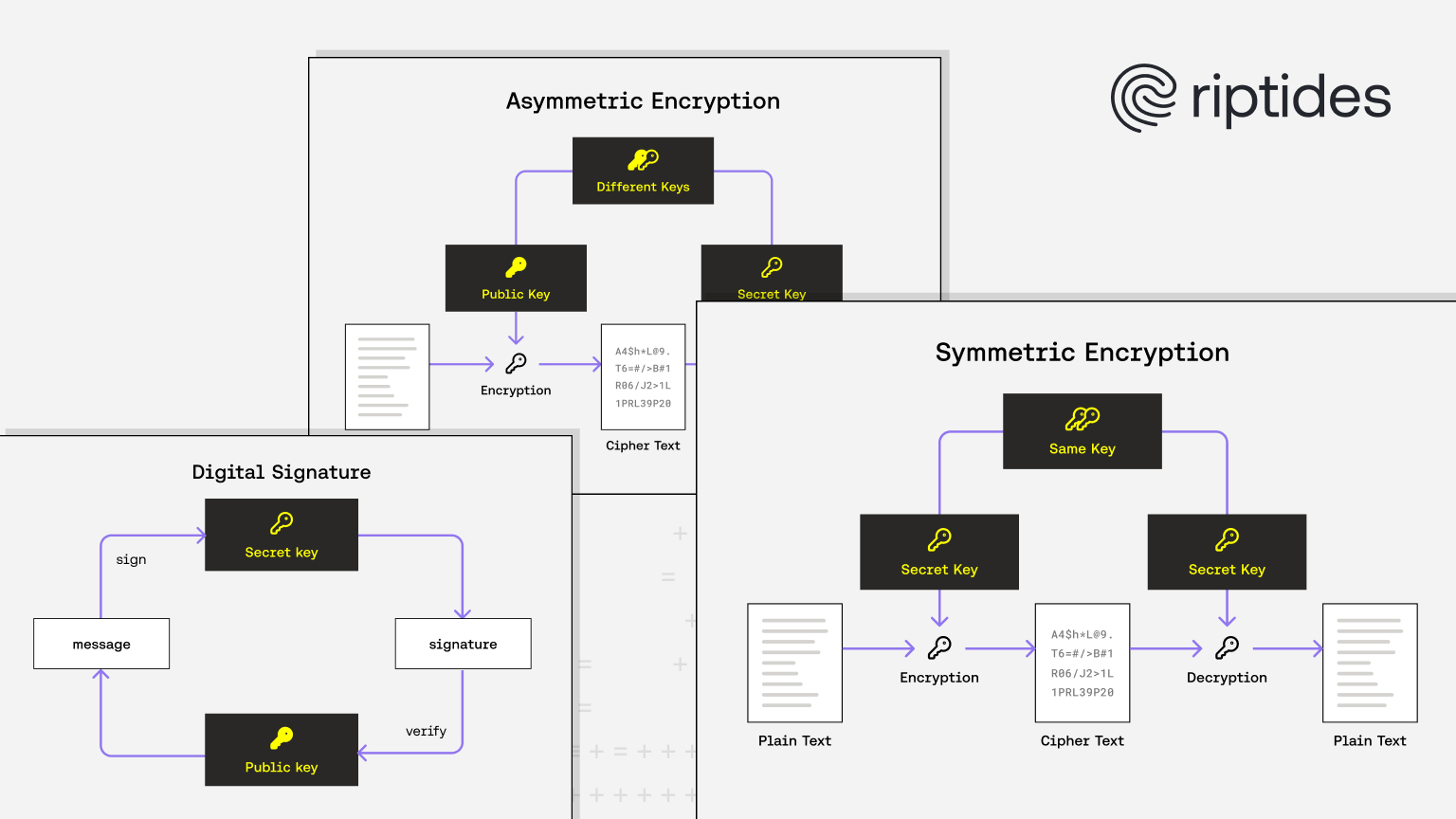
Symmetric Cryptography

In symmetric cryptography, the same key is used for all operations. The main challenge is securely sharing this key between the sender and receiver without exposing it publicly.

Key derivation functions (KDFs) help generate encryption keys from passwords, which are easier for humans to remember. Modern symmetric encryption schemes usually combine multiple algorithms into a single encryption scheme (cipher construction).
For example:

Key derivation algorithm + Symmetric cipher algorithm + Cipher block mode + Message authentication (MAC) algorithm

‍

Examples of combined schemes include: CHACHA20_POLY1305_SHA256 or AES_GCM_256. Typical shared key sizes are 128, 192, or 256 bits. Modern symmetric algorithms include AES and ChaCha20.

We differentiate two modes of symmetric encryption:

• Block Ciphers (AES): Encrypt data in fixed-size blocks.
• Stream Ciphers (ChaCha20): Encrypt data byte by byte as a stream.

For example, when you see AES_GCM_256, it includes multiple components:

• Block-to-stream transformation (GCM): Allows encrypting data of arbitrary size using a block cipher.
• Block Cipher (AES): Encrypts the data blocks securely.
• Message Authentication (MAC): Ensures the decrypted message matches the original and hasn’t been tampered with.

To further enhance security, authenticated encryption combines encryption with a verification code to ensure message integrity. If this scheme is used, decryption success indicates both that the key is valid and the message is untampered.

An even more advanced concept is Authenticated Encryption with Associated Data (AEAD). AEAD binds additional data (associated data) to the ciphertext and context, helping detect attempts to cut and paste encrypted messages between different contexts.

AES

AES stands for Advanced Encryption Standard, also known as Rijndael. It is considered highly secure; although some attacks have been published, there are no known practical exploits. AES is one of the most widely used ciphers in TLS. Modern CPUs often include hardware enhancements to accelerate AES encryption and decryption.

AES is a block cipher with a fixed block size of 128 bits, regardless of the key size. It usually requires an initialization vector (IV) a non-secret, random value used to add variability to the encryption.

During encryption, AES takes the key and input data to produce the ciphertext. The IV is then combined with the ciphertext, and if authenticated encryption (AE) is enabled, a Message Authentication Code (MAC) is also included to ensure integrity.

Decryption works in reverse. The AES decryptor first extracts the IV and uses it with the key to recover the original message. If AE is enabled, the MAC is verified to confirm the message has not been tampered with and that the key is valid.

ChaCha20

ChaCha20 is a highly secure, lightweight 256-bit stream cipher. It uses a 256-bit key along with a 96-bit nonce to encrypt data.

The algorithm first derives an inner key from the user-provided key and nonce, then initializes the cipher and encrypts data blocks sequentially. The ciphertext is produced by XORing the plaintext with the output of the encryption step.

Industry standards recommend using ChaCha20-Poly1305 or AES-256-GCM, as both are highly secure and well-tested. ChaCha20 is roughly three times faster than AES-GCM, which is why it is the default choice in Riptides.

‍

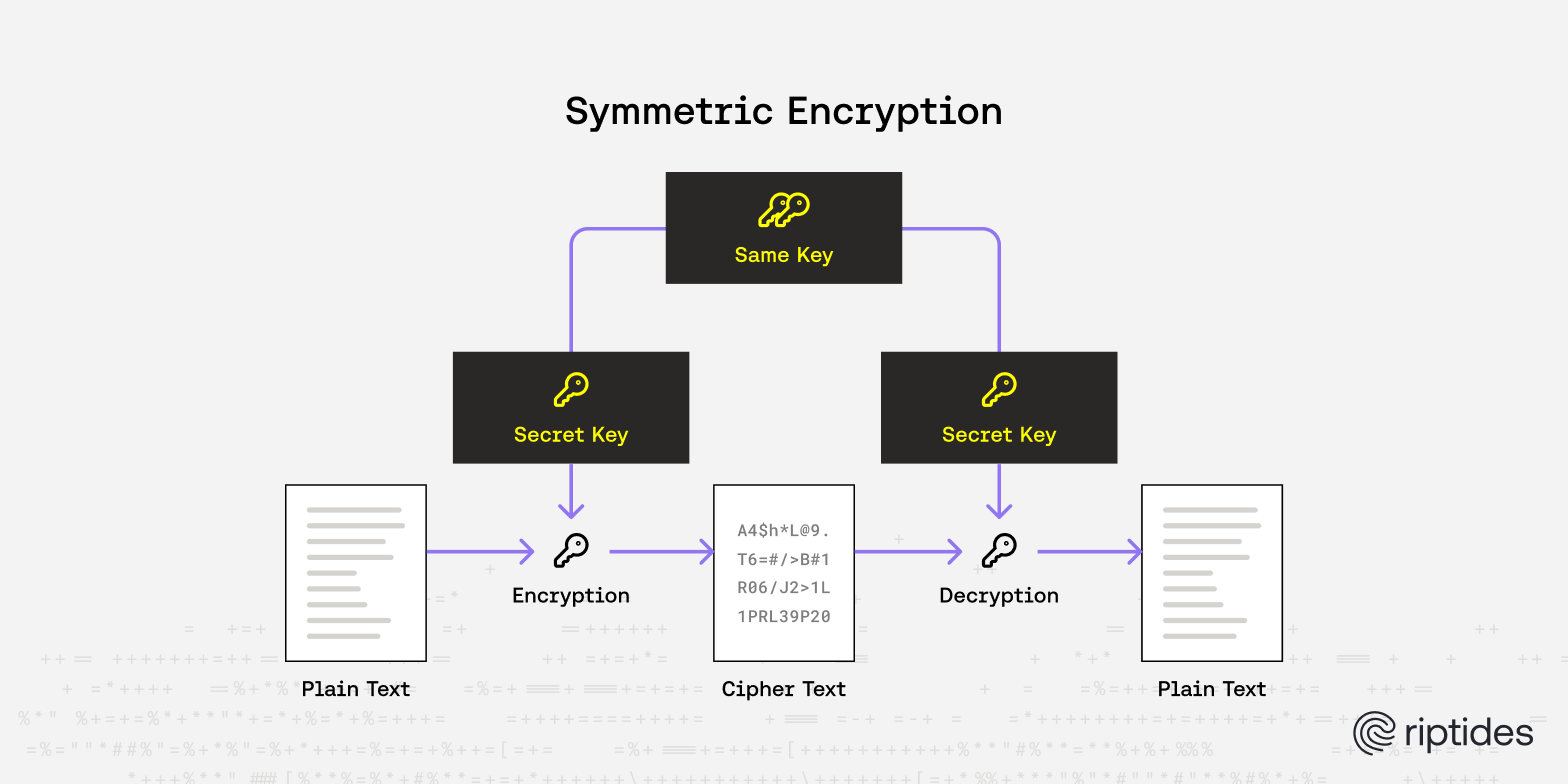
Asymmetric Cryptography / Public Key Cryptography

As mentioned earlier, public key cryptography uses separate keys for encryption and decryption: a public key and a private key, which are mathematically linked. Public key cryptography is not only used for encryption and decryption but also for digital signatures and key exchange.

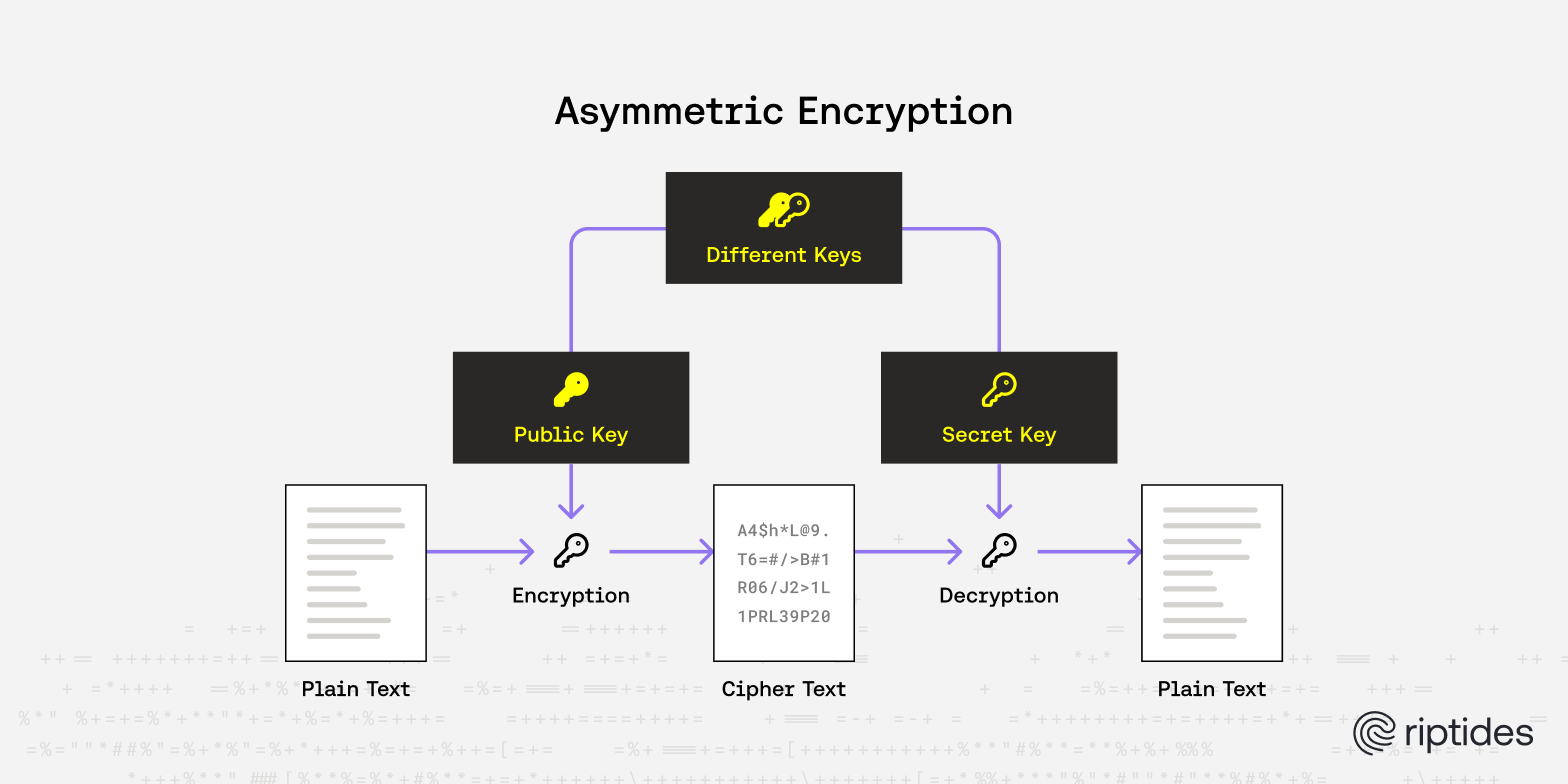
Encrypting data directly with asymmetric algorithms is computationally expensive compared to symmetric cryptography. Typically, a hybrid approach is used:

• A symmetric key is generated to encrypt the message.
• The symmetric key is then encrypted using the recipient’s public key.

For decryption, the recipient first uses their private key to decrypt the symmetric key, and then uses that key to decrypt the message.

Asymmetric cryptography can also be used “in reverse,” where data is encrypted with a private key. This proves the identity of the owner and is the basis for digital signatures.

We distinguish two widely used asymmetric cryptosystems:

RSA

RSA (Rivest-Shamir-Adleman) is one of the earliest public key cryptosystems. It is based on modular exponentiation and the computational difficulty of factoring large integers. In RSA, the public and private keys are generated together. Typical RSA key lengths are 2048, 3072, or 4096 bits. Longer keys offer higher security but require more computation. Keys above 3072 bits are generally considered secure.

RSA key generation involves finding three large integers: e, d, and n, such that:

(x^e)^d ≡ x (mod n)  for all x in [0..n)

‍

• n is the modulus and defines the key length (e.g., 3072 bits).
• (n, e) is the public key, where e (commonly 65537) is the public exponent.
• (n, d) is the private key, where d is the private exponent.

‍

ECC

Elliptic Curve Cryptography (ECC) is a more modern public key cryptosystem based on the elliptic curve discrete logarithm problem a problem as hard as integer factorization.

ECC provides strong security with much smaller keys: a 256-bit ECC key is roughly equivalent to a 3072-bit RSA key. Private keys are simply integers in the range of the curve’s field, making key generation extremely fast. Public keys are points on the curve, represented as coordinate pairs {x, y}.

ECC supports different curves, which offer varying levels of security, performance, and key length. The most commonly used curves are:

• secp256k1
• secp384r1

Both RSA and ECC can be used for:

• Key exchange
• Digital signatures
• Encryption

We’ve already covered encryption; next, let’s look at key exchange and digital signatures, which are also essential for TLS.

Digital Signature

A digital signature is a cryptographic scheme used to verify the authenticity of digital messages or documents. A valid signed document gives the recipient confidence that the message came from a known sender. Think of it like a handwritten signature—but for the digital world.

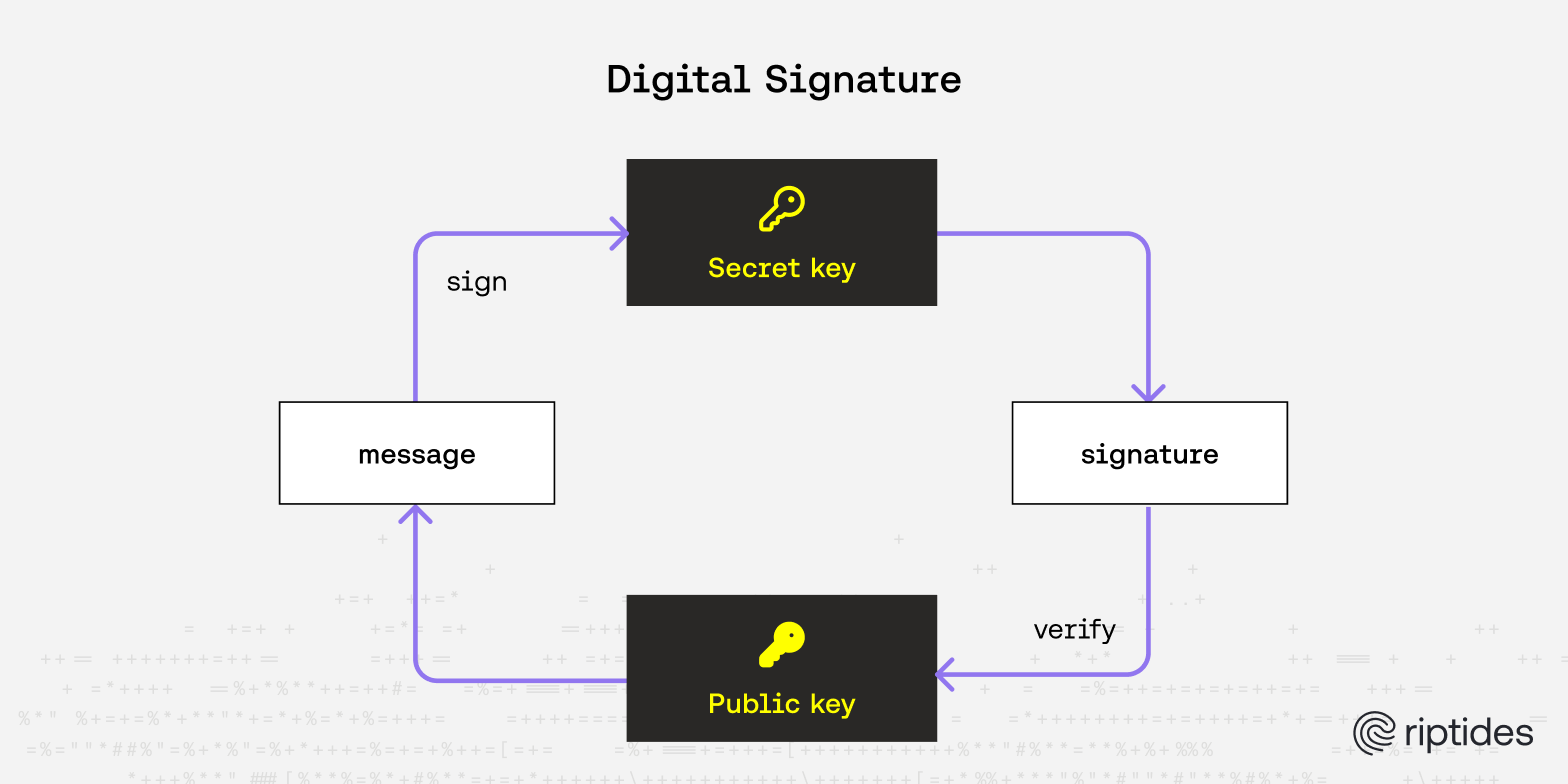
A message is signed using a private key, and the signature can later be verified with the corresponding public key. Signed messages cannot be altered without detection, providing authentication, message integrity, and non-repudiation.

Digital signatures can be implemented using RSA or DSA, while ECC provides an equivalent method called ECDSA.

Key Exchange

Key exchange is the process by which a secret key is securely shared between two parties. It ensures that no one else can access the key, which is essential for establishing secure communication in TLS.

During the TLS handshake, the parties negotiate a secret key that will be used for encryption during the session. This handshake happens millions of times in web browsers every day.

Common key exchange methods include:

• Diffie-Hellman Key Exchange (DHKE): one of the earliest widely used methods.
• Elliptic Curve Diffie-Hellman (ECDH): a more modern, efficient version using elliptic curves.

With this, we now have a basic understanding of the cryptographic building blocks used in TLS. To maximize compatibility, Riptides relies on certificates and TLS using SPIFFE.

ECC vs RSA with Riptides

We recently introduced Elliptic Curve Cryptography (ECC) to Riptides and ran a rough comparison of TLS using RSA and ECC.

For this comparison, we focus on the TLS handshake, as this is where the heavy computation happens. During data transfer, the same symmetric cipher is used, so the main difference in speed comes from the handshake itself.

Setup

For this benchmark, we used a typical developer laptop environment: a MacBook Air with an M3 processor and 16 GB of RAM. Since our benchmarks require Linux, we ran a Lima virtual machine with the default settings and the standard Ubuntu template.

To measure TLS handshake performance, we used Tempesta’s TLS perf tool. This lightweight tool stresses the TLS handshake only and quickly resets TCP connections after each attempt.

The server part of the test is a simple Go HTTP server, with TLS provided using Riptides. For both RSA and ECC tests, we limited parallel connections to 100, used two threads, and ran the benchmark for 10 seconds.

Results

With RSA cryptosystem, we used a 4096-bit RSA key pair with the DHE-RSA-CHACHA20-POLY1305 cipher. Since the library terminates the connection immediately after the handshake, the CHACHA20-POLY1305 symmetric cipher is not relevant here.

For certificate validation and key exchange, the Diffie-Hellman protocol and RSA are used.

With ECC cryptosystem, we used a 384-bit EC key pair with the ECDHE-ECDSA-CHACHA20-POLY1305 cipher. As before, the CHACHA20-POLY1305 symmetric cipher can be ignored since the benchmark focuses on the TLS handshake.

For certificate validation and key exchange, Elliptic Curve Diffie-Hellman (ECDH) and ECDSA are used.

With ECC, we achieved roughly 6.5× faster TLS handshake performance over RSA! Moreover, ECC-384 provides better security than RSA-4096, as it is roughly equivalent to RSA-7680 in terms of cryptographic strength.

Conclusion

In this blog post, we briefly introduced cryptography by exploring different cryptosystems, including symmetric and asymmetric cryptography. While discussing asymmetric cryptography, we compared RSA and ECC, and explained the roles of key exchange and digital signatures. With this foundation, we now understand the cryptographic building blocks behind TLS.

Finally, we gave a rough estimate of Riptides’ performance using RSA and ECC for TLS, showing the significant speed and security benefits of ECC. There are many resources online if you want to dive deeper into cryptography, and we’re also preparing more blog posts on this topic so stay tuned!

If you enjoyed this post, follow us on LinkedIn and X for more updates. If you’d like to see Riptides in action, get in touch with us for a demo.